Poker Odds and Charts Chances of hitting, flopping and holding certain hands. These odds are a must know if you want to advance your game to a high level. For exact odds you can check out our poker hand odds calculator. We rounded the number to the nearest decimal for you. May 23, 2017 There are 2,598,960 many possible 5-card Poker hands. Thus the probability of obtaining any one specific hand is 1 in 2,598,960 (roughly 1 in 2.6 million). The probability of obtaining a given type of hands (e.g. Three of a kind) is the number of possible hands for that type over 2,598,960. Thus this is primarily a counting exercise. For this column, we will restrict ourselves to starting hands from A - A at 35% probability down to Q - 10 off suit at 16% — the 42 best possible starting hands out of a total of 169 non.

See Full List On En.cardmates.net
See Full List On En.cardmates.net
Best scenes casino slots. Brian Alspach
13 January 2000
Abstract:
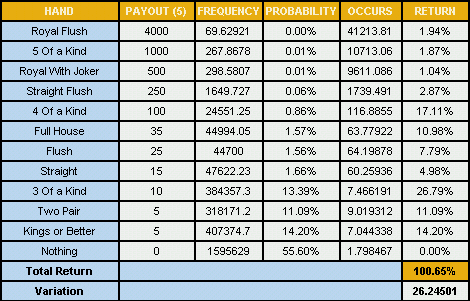
Poker Hand Probability Table Example
The types of 3-card poker hands are
- straight flush
- 3-of-a-kind
- straight
- flush
- a pair
- high card
The total number of 3-card poker hands is .
A straight flush is completely determined once the smallest card in thestraight flush is known. There are 48 cards eligible to be the smallestcard in a straight flush. Hence, there are 48 straight flushes.
In forming a 3-of-a-kind hand, there are 13 choices for the rank and4 choices for the 3 cards of the given rank. This implies there are3-of-a-kind hands.
The ranks of the cards in a straight have the form x,x+1,x+2, wherex can be any of 12 ranks. There are then 4 choices for each card ofthe given ranks. This yields total choices. However,this count includes the straight flushes. Removing the 48 straightflushes leaves us with 720 straights.
To count the number of flushes, we obtain choicesfor 3 cards in the same suit. Of these, 12 are straight flushes whoseremoval leaves 274 flushes of a given suit. Multiplying by 4 produces1,096 flushes.
Now we count the number of hands with a pair. There are 13 choices forthe rank of the pair, and pairs of the chosen rank.The non-pair card can be any of the remaining 48. Thus, thereare 3-card hands with a single pair.
We could determine the number of high card hands by removing the handswhich have already been counted in one of the previous categories.Instead, let us count them independently and see if the numbers sumto 22,100 which will serve as a check on our arithmetic.
A high card hand has 3 distinct ranks, but does not allow ranks of theform x,x+1,x+2 as that would constitute a straight. Thus, there arepossible sets of ranks from which we remove the12 sets of the form .This leaves 274 sets of ranks.For a given set of ranks, there are 4 choices for each cardexcept we cannot choose all in the same suit. Hence, there are274(43-4) = 16,440 high card hands.
If we sum the preceding numbers, we obtain 22,100 and we can be confidentthe numbers are correct.
Here is a table summarizing the number of 3-card poker hands. Theprobability is the probability of having the hand dealt to you whendealt 3 cards.
| hand | number | Probability |
| straight flush | 48 | .0022 |
| 3-of-a-kind | 52 | .0024 |
| straight | 720 | .0326 |
| flush | 1,096 | .0496 |
| pair | 3,744 | .1694 |
| high card | 16,440 | .7439 |
last updated 13 January 2000

